snowbird91 | quite OKNOTOK

quite OKNOTOK

14 Dec 2025

forensics nitectf2025

niteCTF 2025

I played niteCTF 2025 with tjcsc. We got 1st place!

Challenge: quite OKNOTOK
Category: Forensics
Author: teayah
Flag: nite{q01_n0_y0q0an}
Note: We got first blood for this challenge and we were the only team to solve the challenge in the CTF!

My initial read / first impressions

We are given a zip file which only contained one file: binaural_beats with no extension. No other information was given other than an obscure description: “I downloaded a long “binaural” beats audio to help me sleep but it’s been of no use.”
After a bit of googling, I found out that the first 4 bytes of the file were qoaf which is the magic for QOA (Quite OK Audio). So that’s where quite OKNOTOK came from!

Decoding QOA to PCM

So, what is the QOA structure? Well, in a nutshell:

File header: qoaf + total sample count (big-endian).
Then frames. Each frame has:
- 8-byte frame header (channels, sample rate, samples in this frame, frame size).
- LMS predictor state per channel (4 history + 4 weights).
- Packed slices: each slice is 8 bytes = 4-bit scale + 20×3-bit residuals, 20 samples per slice. Channels are interleaved per slice.

I mirrored the reference spec in Python: apply LMS prediction, dequantize with the 16-value table, and rebuild 16-bit PCM. The file was stereo, 44100 Hz. After decoding I saved out.wav just to be sure the audio wasn’t garbage (it sounded like high-pitched warbling instead of sleep music, so THIS is why it’s no use…).

Spotting the modulation: 8 FSK carriers

Short FFTs over the audio (~0.1 s windows) showed eight narrow tones. Each tone hopped between two frequencies 200 Hz apart — classic 2-FSK. The pairs (low/high) were:

7500 / 7700 Hz
8500 / 8700 Hz
9500 / 9700 Hz
10500 / 10700 Hz
11500 / 11700 Hz
12500 / 12700 Hz
13500 / 13700 Hz
14500 / 14700 Hz

With a 0.1 s symbol (4410 samples), each carrier gives 1 bit per symbol. I used Goertzel per (low, high) bin; if energy(high) > energy(low) -> bit = 1 else 0. Collect bits from lowest to highest frequency as MSB -> LSB to form each byte.

A tiny decoder loop:

import numpy as np
from scipy.signal import get_window

RATE = 44100
SYMSZ = int(0.1 * RATE)
carriers = [(7500+200*i, 7700+200*i) for i in range(8)]

def goertzel(x, f):
    k = int(0.5 + (SYMSZ * f) / RATE)
    w = 2*np.pi*k/SYMSZ
    coeff = 2*np.cos(w)
    s0 = s1 = s2 = 0.0
    for v in x:
        s0 = v + coeff*s1 - s2
        s2, s1 = s1, s0
    return s1*s1 + s2*s2 - coeff*s1*s2

pcm = np.fromfile("out.pcm", dtype=np.int16).reshape(-1, 2)[:,0]  # mono
bytes_out = []
for i in range(0, len(pcm), SYMSZ):
    sym = pcm[i:i+SYMSZ]
    if len(sym) < SYMSZ: break
    bits = []
    for lo, hi in carriers:
        e_lo, e_hi = goertzel(sym, lo), goertzel(sym, hi)
        bits.append(1 if e_hi > e_lo else 0)
    b = 0
    for bit in bits:
        b = (b << 1) | bit
    bytes_out.append(b)
open("modem.bin","wb").write(bytes(bytes_out))

modem.bin started with qoif. Jackpot! This is big news! This appears to be a QOI image.

QOI -> hidden.png (there’s a QR hiding on the edge)

Decoding the QOI gave a 150×25 RGB strip.

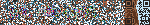
Visually it’s noisy with a faint QR-looking checkerboard on the right 25 columns. The QR was color-dithered enough that normal scanners failed.

I used a small QR reader to crop the rightmost 25×25 square, binarize by luminance, unmask the modules, and parse version-2 QR codewords directly:

#!/usr/bin/env python3
from __future__ import annotations

import sys
from dataclasses import dataclass
from pathlib import Path

import numpy as np
from PIL import Image

def _luminance(rgb: np.ndarray) -> np.ndarray:
    rgb = rgb.astype(np.float32)
    return 0.299 * rgb[..., 0] + 0.587 * rgb[..., 1] + 0.114 * rgb[..., 2]

def binarize_qr(rgb_crop: np.ndarray) -> np.ndarray:
    lum = _luminance(rgb_crop)
    uniq = np.unique(np.round(lum, 3))
    if len(uniq) <= 32 and float(uniq[-1]) > 150.0:
        thr = float(uniq[-2])
        dark = lum < thr
        return dark
    vals = np.clip(lum.astype(np.int32), 0, 255)
    hist = np.bincount(vals.ravel(), minlength=256).astype(np.float64)
    total = vals.size
    sum_total = np.dot(np.arange(256), hist)
    sum_b = 0.0
    w_b = 0.0
    max_var = -1.0
    thr = 128
    for t in range(256):
        w_b += hist[t]
        if w_b == 0:
            continue
        w_f = total - w_b
        if w_f == 0:
            break
        sum_b += t * hist[t]
        m_b = sum_b / w_b
        m_f = (sum_total - sum_b) / w_f
        var_between = w_b * w_f * (m_b - m_f) ** 2
        if var_between > max_var:
            max_var = var_between
            thr = t
    return lum <= thr

ECL_MAP = {
    0b00: "M",
    0b01: "L",
    0b10: "H",
    0b11: "Q",
}

def _format_codeword(ecl_bits: int, mask: int) -> int:
    data = ((ecl_bits & 0x3) << 3) | (mask & 0x7) 
    g = 0x537
    v = data << 10
    for i in range(14, 9, -1):
        if (v >> i) & 1:
            v ^= g << (i - 10)
    remainder = v & 0x3FF
    code = (data << 10) | remainder
    code ^= 0x5412
    return code

FORMAT_TABLE = [(_format_codeword(ecl, m), ecl, m) for ecl in range(4) for m in range(8)]

def read_format_bits_top_left(mod: np.ndarray) -> int:
    bits = []
    for c in range(0, 6):
        bits.append(int(mod[8, c]))
    bits.append(int(mod[8, 7]))
    bits.append(int(mod[8, 8]))
    bits.append(int(mod[7, 8]))
    for r in range(5, -1, -1):
        bits.append(int(mod[r, 8]))
    v = 0
    for b in bits:
        v = (v << 1) | b
    return v

def hamming(a: int, b: int) -> int:
    return (a ^ b).bit_count()

@dataclass
class QRFormat:
    ecl_bits: int
    mask: int

def decode_format(mod: np.ndarray) -> QRFormat:
    v = read_format_bits_top_left(mod)
    best = None
    for code, ecl, mask in FORMAT_TABLE:
        d = hamming(v, code)
        if best is None or d < best[0]:
            best = (d, ecl, mask)
    assert best is not None
    dist, ecl_bits, mask = best
    return QRFormat(ecl_bits=ecl_bits, mask=mask)

def build_function_mask(version: int, N: int) -> np.ndarray:
    func = np.zeros((N, N), dtype=bool)
    finders = [(0, 0), (0, N - 7), (N - 7, 0)]
    for r0, c0 in finders:
        for r in range(r0 - 1, r0 + 8):
            for c in range(c0 - 1, c0 + 8):
                if 0 <= r < N and 0 <= c < N:
                    func[r, c] = True
    func[6, :] = True
    func[:, 6] = True
    if version == 2:
        cy = cx = 18
        for r in range(cy - 2, cy + 3):
            for c in range(cx - 2, cx + 3):
                func[r, c] = True
    func[8, 0:9] = True
    func[0:9, 8] = True
    func[8, N - 8 : N] = True
    func[N - 8 : N, 8] = True
    func[4 * version + 9, 8] = True
    return func

def mask_condition(mask: int, r: int, c: int) -> bool:
    if mask == 0:
        return (r + c) % 2 == 0
    if mask == 1:
        return r % 2 == 0
    if mask == 2:
        return c % 3 == 0
    if mask == 3:
        return (r + c) % 3 == 0
    if mask == 4:
        return ((r // 2) + (c // 3)) % 2 == 0
    if mask == 5:
        return ((r * c) % 2 + (r * c) % 3) == 0
    if mask == 6:
        return (((r * c) % 2 + (r * c) % 3) % 2) == 0
    if mask == 7:
        return (((r + c) % 2 + (r * c) % 3) % 2) == 0
    raise ValueError("invalid mask")

def extract_codewords(mod_dark: np.ndarray, fmt: QRFormat) -> list[int]:
    N = mod_dark.shape[0]
    version = (N - 17) // 4
    func = build_function_mask(version, N)
    m = mod_dark.copy().astype(np.uint8)
    for r in range(N):
        for c in range(N):
            if func[r, c]:
                continue
            if mask_condition(fmt.mask, r, c):
                m[r, c] ^= 1
    bits: list[int] = []
    col = N - 1
    upward = True
    while col > 0:
        if col == 6:
            col -= 1
        rows = range(N - 1, -1, -1) if upward else range(N)
        for r in rows:
            for c in (col, col - 1):
                if func[r, c]:
                    continue
                bits.append(int(m[r, c]))
        upward = not upward
        col -= 2
    codewords: list[int] = []
    for i in range(0, len(bits) // 8 * 8, 8):
        b = 0
        for j in range(8):
            b = (b << 1) | bits[i + j]
        codewords.append(b)
    return codewords

def decode_qr_payload(mod_dark: np.ndarray) -> str:
    fmt = decode_format(mod_dark)
    codewords = extract_codewords(mod_dark, fmt)
    data_cw = codewords[:28]  
    bits = []
    for b in data_cw:
        for i in range(7, -1, -1):
            bits.append((b >> i) & 1)
    def read(n: int) -> int:
        nonlocal bits
        v = 0
        for _ in range(n):
            v = (v << 1) | bits.pop(0)
        return v
    length = read(8)  
    out = bytearray()
    for _ in range(length):
        out.append(read(8))
    return out.decode("utf-8", errors="replace")

def main() -> int:
    img_path = Path(sys.argv[1])
    rgb = np.array(Image.open(img_path).convert("RGB"))
    h, w, _ = rgb.shape
    crop = rgb[:, w - h : w, :]
    mod_dark = binarize_qr(crop)
    payload = decode_qr_payload(mod_dark)
    print(payload)
    return 0

if __name__ == "__main__":
    raise SystemExit(main())

Run it:

python3 qr_decode_from_hidden.py hidden.png
# -> pastebin.com/kdhd1pSD

The Pastebin (how many parts are there?!)

Opening the Pastebin link gives you this

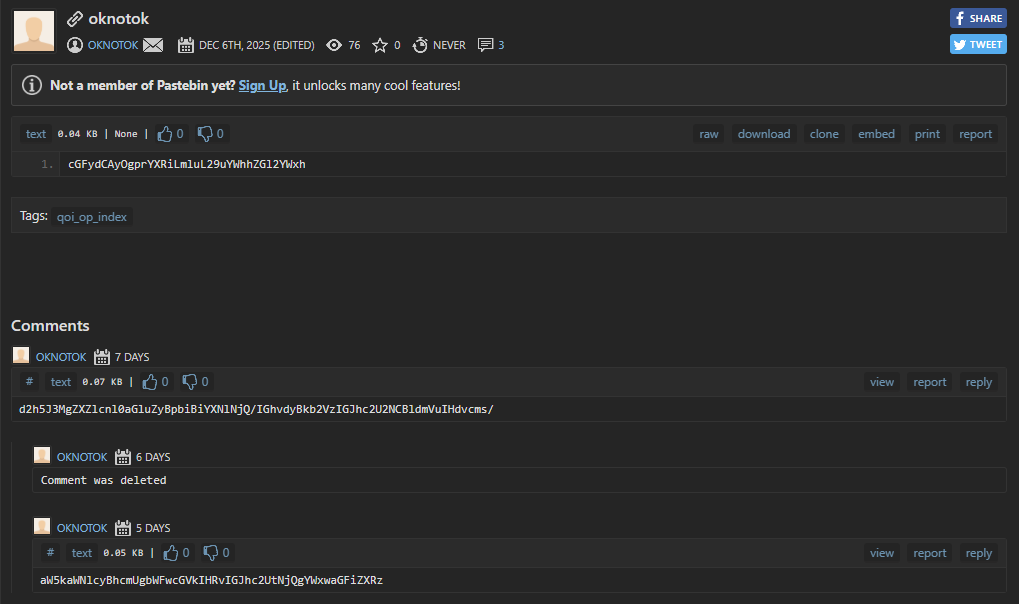
We have three ciphertexts:

cGFydCAyOgprYXRiLmluL29uYWhhZGl2YWxh
d2h5J3MgZXZlcnl0aGluZyBpbiBiYXNlNjQ/IGhvdyBkb2VzIGJhc2U2NCBldmVuIHdvcms/
aW5kaWNlcyBhcmUgbWFwcGVkIHRvIGJhc2UtNjQgYWxwaGFiZXRz

Decoding them from Base64 resulted in:

part 2: katb.in/onahadivala
why's everything in base64? how does base64 even work?
indices are mapped to base-64 alphabets

Hmm, interesting. The second and third seem to be clues. What is the first link about..?

The katb.in detour: another QOI and a column hash

The katb page held a huge <code> block. Pulling it and base64-decoding produced another QOI (data.bin). Decoding that gave a second 150×24-ish image.

It appears to say p2: rgba. How do I use this?

At this point we stopped treating the second QOI as “just an image” and read the QOI spec. QOI decoders maintain a 64-slot pixel cache, and every decoded pixel is inserted at a deterministic index:
- idx = (r*3 + g*5 + b*7 + a*11) % 64
That produces values in the range 0-63, which matched the Pastebin hints (“indices are mapped to base‑64 alphabets” and “Tags: qoi_op_index”). So we took the rightmost column’s pixels, computed this QOI index for each one, mapped 0-63 through the Base64 alphabet, and base64-decoded the resulting string to get:

part 2: n0_y0q0an}

So we now had the tail of the flag. We just have to find the first half!

Reconstructing the front half

Comparing hidden.png (from the audio) and decoded1.png (from katb) showed almost identical “snow,” except a few colored specks in hidden.png. A light Gaussian blur over those differences spelled out:

nite{q01

Cool! I see the first half and the second half. Stitching the two halves together gave the full flag: nite{q01_n0_y0q0an}. Woo! That was a fun challenge, and we got first blood!

Takeaways

Study QR codes, they are super fascinating!
Steganography can be as simple as “two almost-identical images, blur the difference.”

Thank you for reading my write-up! This was an extremely fun CTF, and I would like to express my appreciation to the organizers for hosting the CTF!

If there’s anything you think I could improve on in future write-ups, please let me know!

Thank you and have a great day!